Gleisplanberechung mit Vektoren

Unzufrieden mit der Option "Gleise automatisch verbinden" bei Wintrack, die sehr selten ein brauchbares Resultat liefert, und genervt vom umständlichen Rechnen mit Sinus und Cosinus ging ich dazu über, Gleisfiguren mit Vektoren zu berechnen. Anstatt jedesmal einzeln die trigonometrischen Funktionen anzusetzen, kann man mit Vektoren nach Schema F rechnen.

Natürlich rechnet man nicht selbst, sondern überlässt das dem Rechner. Eine Tabellenkalkulation liefert für jede Gleisfigur die gewünschten Daten. Zusammen mit den praktischen Längentabellen von bogobit.de findet man schnell alle sinnvollen Kombinationen für den gewünschten Gleisplan heraus.

Wie man ein Gleis darstellt

Um ein Gleis zu beschreiben braucht man lediglich X- und Y-Koordinate. Diese werden in einem Vektor zusammengefasst. Noch ist die Lage unseres Gleises im Raum unbekannt. Man spart sich Rechenaufwand, wenn man ein Gleis einfach als in X-Richtung ausgerichtet betrachtet.

Formel für ein gerades Gleis, hier mit 188,3 mm Länge

Für gebogene Gleise kommt dazu noch eine Abweichung in Y-Richtung, die durch die Krümmung bedingt ist. Bei einer Krümmung nach links verwendet man für Radius (r) und Winkel (β) positive Vorzeichen, bei einer Krümmung nach rechts negative.

Formel für ein gebogenes Gleis, hier mit 360 mm Radius und einem Winkel von 30°

Für Weichen ist keine eigene Formel nötig. Man wählt die für Geraden oder für Bögen, je nachdem welchen Fahrweg man betrachtet. Bogenweichen und Kreuzungen werden weiter unten betrachtet.

Vom Gleis zum Gleisplan

Zwei aneinandergesteckte Gleise berechnet man, indem man ihre Vektoren addiert. Das geht noch ganz einfach:

Addition zweier Vektoren durch Addition ihrer Komponenten

Ein wenig komplizierter wird es, wenn Krümmungen ins Spiel kommen. Dazu ist eine Drehmatrix nötig. In die Drehmatrix setzt man als Winkel die Summe der Winkel aller vorherigen Gleise ein. Die Multiplikation eines Vektors mit einer Matrix folgt einem immergleichen Schema. Bei ihr gilt allerdings kein Kommutativgesetz, d.h. man darf die Reihenfolge von Matrix und Vektor nicht ändern.

Drehung eines Vektors um den Winkel α durch Multiplikation mit der Drehmatrix

Man kann auch Matrizen miteinander multiplizieren und erhält eine neue Matrix. Die Drehmatrix verhält sich dabei äußerst zahm. Zwei Drehmatrizen erfüllen sogar miteinander das Kommutativgesetz. Bevor man aber einen Vektor zweimal dreht, addiert man besser die Winkel beider Drehungen und setzt sie in eine neue Drehmatrix ein.

Produkt zweier Drehmatrizen

Dazu ein Beispiel

[Beispiel in Vorbereitung]

Gelegentlich stimmen die berechneten Werte nicht exakt mit denen aus dem Märklinkatalog überein. Es handelt sich dann um Rundungsfehler.

Kreuzungen und Kreuzungsweichen

Eine alternative Form, Kreuzungen zu berechnen, setzt die Winkel und die Länge der geraden Gleise als bekannt voraus. Den Radius einer Kreuzungsweiche braucht man nicht zu kennen. Man stellt die Kreuzung als zwei gerade Gleise dar mit einem Bogen des Radius 0 in der Mitte.

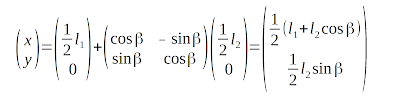Formel für eine drehsymmetrische Kreuzung des Winkels β

Diese Methode funktioniert auch bei Kreuzungen mit unterschiedlich langen Geraden, beispielsweise beim Profigleis von Fleischmann.

Bogenweichen

Die übliche Form von Bogenweichen hat einen inneren Bogen, der wie ein gewöhnliches gebogenes Gleis behandelt werden kann, und einen äußeren, der aus einer Geraden und einem Bogen zusammengesetzt ist.

Formel für eine den äußeren Bogen einer Innenbogenweiche
mit der Zwischengeraden l, Radius r und Winkel β

Man gibt die Vektoren am besten einzeln ein. 

Überführung in eine Tabellenkalkulation

Die Tabelle kann im Downloadbereich gefunden werden. In der xml-Variante geht leider beim Abspeichern ein Teil der Formatierung verloren. Der Nutzer sollte sie in ein geeignetes Dateiformat umwandeln, das zu dem von ihm genutzten Tabellenkalkulationsprogramm passt. Das Original wurde mit LibreOffice Calc erstellt.

Das obige Beispiel, in die Tabelle eingetragen
(Anklicken zum Vergrößern)

Die Startkoordinaten werden links oben eingetragen, die Gleise unten. Oben erscheinen dann die Koordinaten, an denen das Gleis endet.

Verwandte Artikel

Kleine Gleisplansammlung